Intro
Discover 5 ways to find unit conversions, measurements, and calculations with ease, using online tools, formulas, and conversion charts for length, weight, and volume units.
The concept of finding units is crucial in various mathematical and real-world applications. Units can refer to the basic building blocks of measurement, such as meters for length or grams for mass, or they can represent individual items in a collection. Understanding how to find units efficiently is essential for problem-solving in fields like physics, engineering, and even everyday calculations. Here, we'll delve into five ways to find units, exploring the methods, their applications, and the importance of precision in these calculations.
Finding units can be approached from different angles, depending on the context of the problem. For instance, in physics, finding the unit of a derived quantity involves understanding the fundamental units of measurement and how they combine. In mathematics, particularly in algebra, finding the unit of a polynomial or a matrix involves specific operations that yield a result with certain properties. Let's explore these methods in detail, starting with the basic principles of measurement and calculation.
The importance of accurately finding units cannot be overstated. In science and engineering, incorrect units can lead to misunderstandings, miscalculations, and potentially dangerous outcomes. For example, in aerospace engineering, the difference between meters and feet can be critical when calculating trajectories or structural loads. Similarly, in chemistry, understanding the units of measurement for substances is vital for mixing compounds safely and effectively.
Understanding Basic Units of Measurement

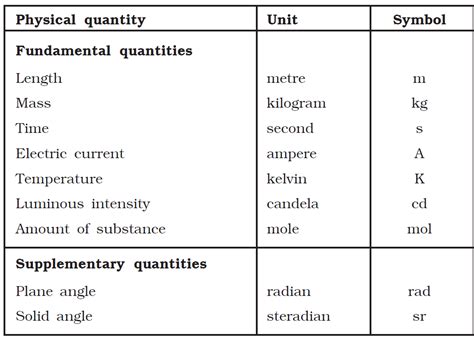
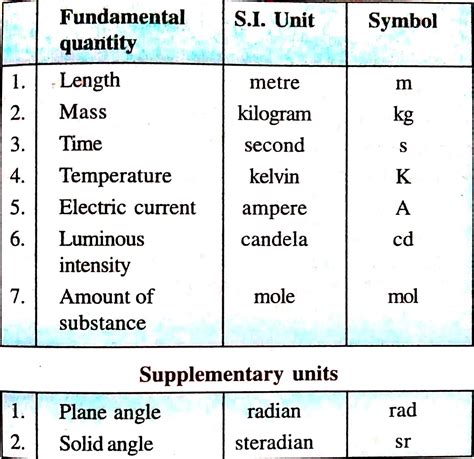
The first step in finding units involves a solid grasp of the basic units of measurement. The International System of Units (SI) provides a standardized framework, including units like the meter for length, the kilogram for mass, and the second for time. Understanding how these units are defined and how they are used to derive other units is fundamental. For instance, the unit of speed is derived from the units of distance (meters) and time (seconds), resulting in meters per second (m/s).
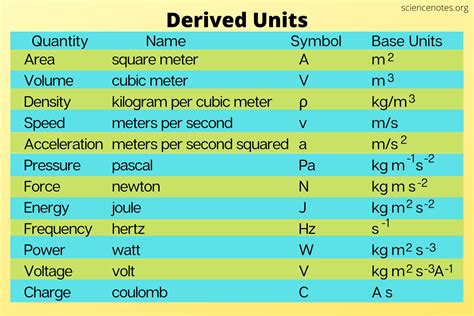
Derived Units and Calculations
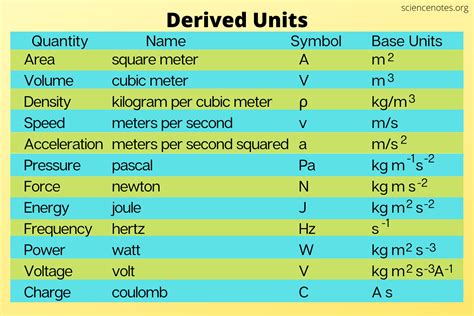
Derived units are those that can be expressed in terms of the basic units. Examples include the unit of force (Newtons), which is derived from the units of mass (kilograms), acceleration (meters per second squared), and the unit of energy (Joules), which can be expressed in terms of force (Newtons) and distance (meters). Calculating derived units involves multiplying or dividing the basic units according to the formula that defines the derived quantity. This process requires careful attention to the units involved to ensure that the final result has the correct unit.
Algebraic Methods for Finding Units
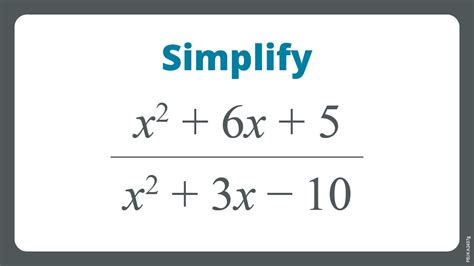
In algebra, finding units can refer to identifying the multiplicative identity in a set of elements under a specific operation. For polynomials, the unit is a polynomial that, when multiplied by any other polynomial, yields that same polynomial. In matrix algebra, the unit matrix (or identity matrix) is a square matrix that, when multiplied by another matrix, leaves the latter unchanged. Algebraic methods for finding units involve solving equations where the unknown is the unit element, which satisfies the condition of leaving other elements unchanged under the operation.
Applications in Real-World Scenarios
- Physics and Engineering: Understanding how to find and manipulate units is crucial for solving problems in mechanics, electromagnetism, and thermodynamics.
- Data Analysis: In statistics and data science, identifying the unit of observation (the individual item being measured) is key to accurate analysis and interpretation of data.
- Computer Science: In programming, understanding units can refer to managing individual elements of data or code, such as bytes in a dataset or individual instructions in a program.
Practical Examples and Calculations
To illustrate the process of finding units in practice, consider the calculation of the area of a room. If the length of the room is measured in meters and the width is also in meters, the unit of area (square meters) is found by multiplying the units of length and width. This straightforward example demonstrates how understanding the basic units and how they combine is essential for performing calculations correctly.
Advanced Techniques and Considerations

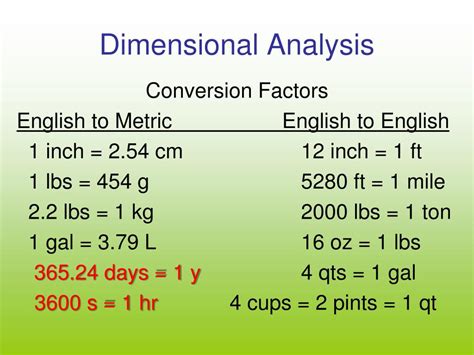
In more complex scenarios, finding units might involve dealing with dimensional analysis, where the focus is on the physical dimensions of quantities rather than their specific units. This approach is useful for checking the consistency of equations and for solving problems where the units are not immediately apparent. Additionally, in fields like quantum mechanics, the concept of units can become abstract, involving not just physical measurements but also theoretical constructs like wave functions and probabilities.
Challenges and Solutions
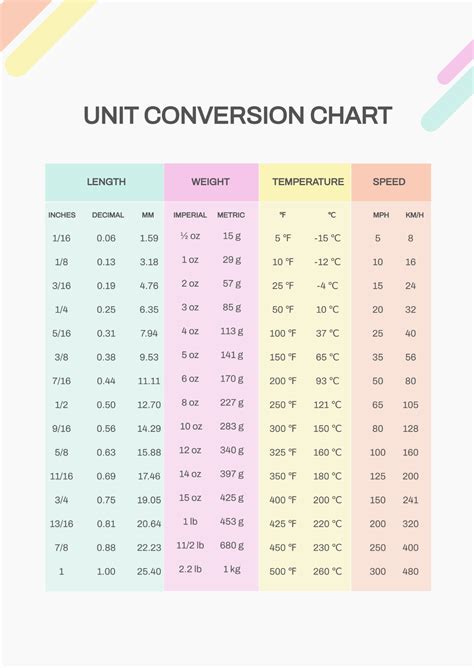
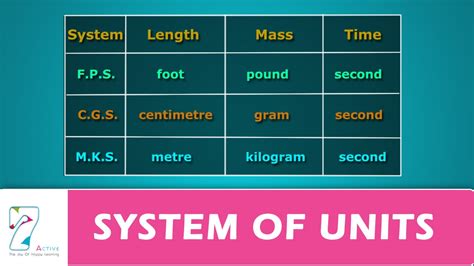
- Unit Conversion: One of the challenges in finding units is converting between different systems of measurement. Solutions involve using conversion factors that relate the units in the two systems.
- Dimensional Analysis: This technique is invaluable for solving problems involving multiple physical quantities and units. It ensures that the final result has the correct units, providing a check on the calculation's validity.
Gallery of Unit-Related Keywords
Unit-Related Keywords Image Gallery


Frequently Asked Questions
What is the importance of finding units in calculations?
+Finding units is crucial for ensuring that calculations are performed correctly and that the results are meaningful and applicable to the real world. Incorrect units can lead to misunderstandings and errors in fields like science, engineering, and economics.
How do derived units differ from basic units?
+Derived units are quantities that can be expressed in terms of the basic units. They are used to describe physical quantities that are not covered by the basic units alone, such as speed, force, and energy. Derived units are calculated by combining basic units according to the formula that defines the derived quantity.
What role does dimensional analysis play in finding units?
+Dimensional analysis is a method used to solve problems involving physical quantities with different units. It ensures that the final result of a calculation has the correct units, providing a check on the calculation's validity and helping to avoid errors due to unit mismatches.
In conclusion, finding units is a fundamental skill that underpins a wide range of mathematical, scientific, and engineering applications. By understanding the basic units of measurement, how to derive new units from them, and how to apply these principles in calculations, individuals can solve problems more accurately and make informed decisions in their fields. Whether dealing with the intricacies of quantum mechanics or the practicalities of building design, the ability to find and manipulate units is an essential tool. As we continue to advance in science and technology, the importance of precise unit analysis will only continue to grow, making it a critical area of study and practice for professionals and students alike. We invite you to share your thoughts on the importance of finding units in the comments below and to explore more topics related to measurement and calculation.
