Intro
Master Calculus 3 with George Masons guide, covering multivariable functions, differential equations, and vector calculus, with tips on optimization, integration, and series convergence.
Calculus 3, also known as Multivariable Calculus, is a fundamental course in mathematics that builds upon the concepts learned in Calculus 1 and 2. At George Mason University, this course is designed to provide students with a comprehensive understanding of the subject, including vectors, partial derivatives, double and triple integrals, and vector calculus. In this article, we will delve into the world of Calculus 3, exploring its importance, key concepts, and providing a study guide for students.
The study of Calculus 3 is crucial for students pursuing careers in mathematics, physics, engineering, and computer science. It provides a strong foundation for understanding complex phenomena in these fields, such as the motion of objects in space, the behavior of electrical circuits, and the optimization of systems. Moreover, the problem-solving skills and analytical thinking developed through the study of Calculus 3 are highly valued by employers across various industries.
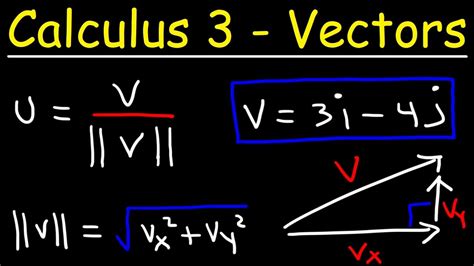
As students embark on their journey through Calculus 3, they will encounter a range of new and challenging concepts. One of the primary focuses of the course is the study of vectors, which are mathematical objects that possess both magnitude and direction. Students will learn how to perform operations with vectors, such as addition, scalar multiplication, and dot products, and how to apply these concepts to solve problems in physics and engineering.
Introduction to Vectors

In addition to vectors, students will also explore the concept of partial derivatives, which are used to study the behavior of functions of multiple variables. This includes learning how to compute partial derivatives, understand their geometric interpretation, and apply them to solve optimization problems.
Partial Derivatives

Another critical component of Calculus 3 is the study of double and triple integrals, which are used to calculate the volume of solids and the surface area of curves. Students will learn how to evaluate these integrals using various techniques, such as substitution, iteration, and polar coordinates.
Double and Triple Integrals

Vector calculus is another essential topic in Calculus 3, which involves the study of vector-valued functions and their properties. Students will learn about the gradient, divergence, and curl of vector fields and how to apply these concepts to solve problems in physics and engineering.
Vector Calculus

To succeed in Calculus 3, students should develop a deep understanding of the underlying concepts and be able to apply them to solve problems. Here are some tips for studying Calculus 3:
- Start by reviewing the material from Calculus 1 and 2, including limits, derivatives, and integrals.
- Practice solving problems regularly, using online resources or textbooks such as Michael Spivak's "Calculus" or James Stewart's "Calculus: Early Transcendentals".
- Watch video lectures or online tutorials to supplement your learning, such as those found on Khan Academy or MIT OpenCourseWare.
- Join a study group or find a study partner to collaborate on problem sets and discuss challenging topics.
Study Tips for Calculus 3

In addition to these general tips, students should also focus on developing their problem-solving skills, which are critical for success in Calculus 3. This includes learning how to:
- Read and understand complex problems
- Identify the key concepts and formulas required to solve the problem
- Apply mathematical techniques, such as substitution or integration by parts, to solve the problem
- Check your work and verify your solutions
Problem-Solving Strategies

Some common applications of Calculus 3 include:
- Physics: Calculus 3 is used to describe the motion of objects in space, including the trajectory of projectiles and the behavior of electrical circuits.
- Engineering: Calculus 3 is used to design and optimize systems, such as bridges, buildings, and electronic circuits.
- Computer Science: Calculus 3 is used in computer graphics, game development, and scientific computing.
Applications of Calculus 3
In conclusion, Calculus 3 is a fundamental course that provides students with a comprehensive understanding of vectors, partial derivatives, double and triple integrals, and vector calculus. By developing a deep understanding of these concepts and applying them to solve problems, students can succeed in Calculus 3 and prepare themselves for careers in mathematics, physics, engineering, and computer science.
Gallery of Calculus 3 Topics
Calculus 3 Image Gallery









What are the main topics covered in Calculus 3?
+The main topics covered in Calculus 3 include vectors, partial derivatives, double and triple integrals, and vector calculus.
How can I prepare for Calculus 3?
+To prepare for Calculus 3, review the material from Calculus 1 and 2, practice solving problems regularly, and watch video lectures or online tutorials to supplement your learning.
What are some common applications of Calculus 3?
+Calculus 3 has many applications in physics, engineering, computer science, and other fields, including the design and optimization of systems, the description of the motion of objects in space, and the behavior of electrical circuits.
How can I succeed in Calculus 3?
+To succeed in Calculus 3, develop a deep understanding of the underlying concepts, practice solving problems regularly, and apply mathematical techniques to solve problems.
What resources are available to help me learn Calculus 3?
+There are many resources available to help you learn Calculus 3, including textbooks, online tutorials, video lectures, and study groups.
We hope this article has provided you with a comprehensive guide to Calculus 3 at George Mason University. Remember to stay focused, practice regularly, and apply mathematical techniques to solve problems. With dedication and hard work, you can succeed in Calculus 3 and prepare yourself for a career in mathematics, physics, engineering, or computer science. If you have any questions or need further assistance, don't hesitate to reach out to your instructor or teaching assistant. Share this article with your friends and classmates, and let's work together to master Calculus 3!
