Intro
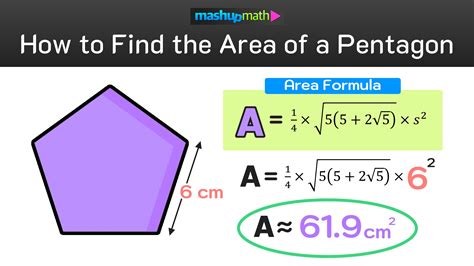
Calculate the area of a pentagon using the Pentagon Area Equation Formula, involving apothem, side length, and perimeter, to find the exact area with precision geometry and trigonometry.
The Pentagon area equation formula is a fundamental concept in geometry, essential for calculating the area of a pentagon, a five-sided polygon. Understanding this formula is crucial for various applications in architecture, engineering, and design. The importance of calculating the area of a pentagon lies in its ability to help professionals and individuals determine the size and scale of structures, spaces, and objects. In this article, we will delve into the world of pentagons, exploring their properties, the formula for calculating their area, and providing examples to illustrate the practical applications of this knowledge.
The pentagon is a unique geometric shape, with five sides and five angles. The sum of the interior angles of a pentagon is 540 degrees, and the sum of the exterior angles is 360 degrees. Pentagons can be regular or irregular, with regular pentagons having all sides and angles equal. The regular pentagon is a particularly interesting shape, with applications in art, architecture, and nature. The formula for calculating the area of a regular pentagon is relatively straightforward, but calculating the area of an irregular pentagon can be more complex.
To calculate the area of a pentagon, we need to understand the different types of pentagons and their properties. A regular pentagon has all sides and angles equal, making it a symmetrical shape. An irregular pentagon, on the other hand, has sides and angles of different lengths and measures. The formula for calculating the area of a regular pentagon is based on the length of one side, while the formula for an irregular pentagon requires more information, such as the lengths of all sides and the measures of all angles.
Understanding the Pentagon Area Equation Formula
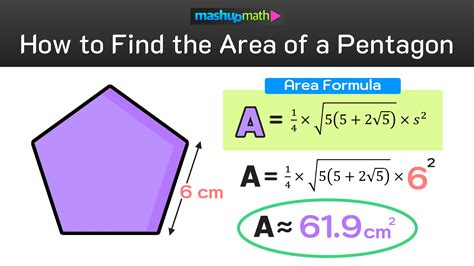
The pentagon area equation formula is a mathematical expression that calculates the area of a pentagon based on its properties. The formula for a regular pentagon is: Area = (n * s^2) / (4 * tan(π/n)), where n is the number of sides (5 for a pentagon), s is the length of one side, and π is a mathematical constant representing the ratio of a circle's circumference to its diameter. For an irregular pentagon, the formula is more complex and requires the use of trigonometry and geometry.
Breaking Down the Formula
The formula for calculating the area of a regular pentagon can be broken down into several components. The first component is the number of sides, which is 5 for a pentagon. The second component is the length of one side, which can be any value. The third component is the mathematical constant π, which is approximately 3.14159. The formula also involves the use of the tangent function, which is a trigonometric function that relates the ratio of the opposite side to the adjacent side in a right triangle.Calculating the Area of a Regular Pentagon

To calculate the area of a regular pentagon, we can use the formula: Area = (n * s^2) / (4 * tan(π/n)). For example, if we have a regular pentagon with a side length of 10 units, we can plug this value into the formula to get: Area = (5 * 10^2) / (4 * tan(π/5)). Using a calculator to compute the value of tan(π/5), we get approximately 0.7265. Plugging this value back into the formula, we get: Area = (5 * 100) / (4 * 0.7265) = 500 / 2.906 = approximately 172.05 square units.
Calculating the Area of an Irregular Pentagon
Calculating the area of an irregular pentagon is more complex and requires the use of trigonometry and geometry. One method for calculating the area of an irregular pentagon is to divide the pentagon into smaller shapes, such as triangles and rectangles, and then calculate the area of each shape separately. The total area of the pentagon is then the sum of the areas of the smaller shapes.Practical Applications of the Pentagon Area Equation Formula

The pentagon area equation formula has numerous practical applications in various fields, including architecture, engineering, and design. For example, architects use the formula to calculate the area of buildings and structures with pentagonal shapes. Engineers use the formula to calculate the area of mechanical components and systems with pentagonal shapes. Designers use the formula to calculate the area of graphical elements and shapes with pentagonal forms.
Real-World Examples
One real-world example of the practical application of the pentagon area equation formula is in the design of the Pentagon building in Washington D.C. The building's shape is a regular pentagon, with five sides of equal length. The area of the building can be calculated using the formula: Area = (n \* s^2) / (4 \* tan(π/n)), where n is the number of sides (5 for a pentagon) and s is the length of one side.Gallery of Pentagon-Related Images
Pentagon Image Gallery






Frequently Asked Questions
What is the formula for calculating the area of a regular pentagon?
+The formula for calculating the area of a regular pentagon is: Area = (n \* s^2) / (4 \* tan(π/n)), where n is the number of sides (5 for a pentagon) and s is the length of one side.
How do I calculate the area of an irregular pentagon?
+To calculate the area of an irregular pentagon, you can divide the pentagon into smaller shapes, such as triangles and rectangles, and then calculate the area of each shape separately. The total area of the pentagon is then the sum of the areas of the smaller shapes.
What are some practical applications of the pentagon area equation formula?
+The pentagon area equation formula has numerous practical applications in various fields, including architecture, engineering, and design. For example, architects use the formula to calculate the area of buildings and structures with pentagonal shapes. Engineers use the formula to calculate the area of mechanical components and systems with pentagonal shapes. Designers use the formula to calculate the area of graphical elements and shapes with pentagonal forms.
Can I use the pentagon area equation formula to calculate the area of other polygons?
+No, the pentagon area equation formula is specific to pentagons and cannot be used to calculate the area of other polygons. However, there are similar formulas for calculating the area of other regular polygons, such as the hexagon and the heptagon.
How do I calculate the perimeter of a pentagon?
+To calculate the perimeter of a pentagon, you need to add up the lengths of all five sides. The formula for the perimeter of a pentagon is: Perimeter = s1 + s2 + s3 + s4 + s5, where s1, s2, s3, s4, and s5 are the lengths of the five sides.
In conclusion, the pentagon area equation formula is a powerful tool for calculating the area of pentagons, with numerous practical applications in various fields. By understanding the formula and its components, individuals can calculate the area of regular and irregular pentagons with ease. Whether you are an architect, engineer, designer, or simply a geometry enthusiast, the pentagon area equation formula is an essential concept to master. We hope this article has provided you with a comprehensive understanding of the pentagon area equation formula and its applications. If you have any further questions or would like to share your experiences with calculating the area of pentagons, please feel free to comment below.
