6 Goes Into 18

The concept of division and fractions is a fundamental part of mathematics, and understanding how numbers interact with each other is crucial for problem-solving and critical thinking. The idea that 6 goes into 18 is a simple yet powerful concept that can help us understand the basics of division and fractions. In this article, we will delve into the world of mathematics and explore the concept of division, fractions, and how 6 goes into 18.

The concept of division is a basic mathematical operation that involves sharing or grouping a certain quantity into equal parts. It is denoted by the symbol ÷ and is used to find the quotient or result of sharing a certain quantity into equal parts. For example, if we have 18 cookies and we want to share them equally among 6 people, we can use division to find out how many cookies each person will get. In this case, 6 goes into 18 exactly 3 times, since 18 ÷ 6 = 3.

Division is an essential concept in mathematics, and it has numerous applications in real-life situations. From sharing food or toys among friends to calculating the cost of goods or services, division is an indispensable tool that helps us make sense of the world around us. Moreover, understanding division is crucial for more advanced mathematical concepts, such as fractions, decimals, and algebra.

Understanding Fractions

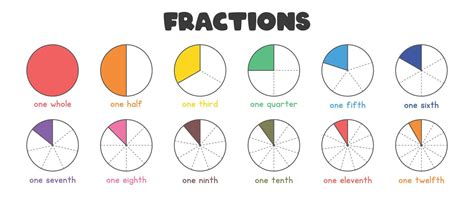
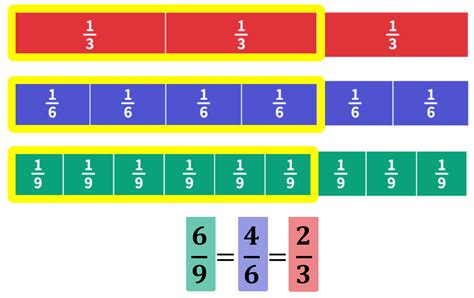
Fractions are a way of representing a part of a whole, and they are denoted by the symbol /. For example, the fraction 1/2 represents one part out of two equal parts. Fractions can be used to represent a wide range of quantities, from measuring ingredients for a recipe to calculating the probability of an event. In the case of 6 going into 18, we can represent this concept as a fraction, where 6 is the denominator and 18 is the numerator. This fraction can be simplified to 1/3, which means that 6 goes into 18 exactly 3 times.

Benefits of Understanding Division and Fractions

Understanding division and fractions has numerous benefits, from improving problem-solving skills to enhancing critical thinking. By mastering these concepts, individuals can develop a deeper understanding of mathematical relationships and apply them to real-life situations. Moreover, division and fractions are essential for more advanced mathematical concepts, such as algebra and geometry, which are critical for careers in science, technology, engineering, and mathematics (STEM).

Some of the benefits of understanding division and fractions include:

Improved problem-solving skills: Division and fractions help individuals develop critical thinking and problem-solving skills, which are essential for real-life situations.
Enhanced critical thinking: By understanding division and fractions, individuals can develop a deeper understanding of mathematical relationships and apply them to complex problems.
Better decision-making: Division and fractions can help individuals make informed decisions, from calculating the cost of goods or services to evaluating the risk of an investment.
Increased career opportunities: Mastery of division and fractions is essential for careers in STEM, which are in high demand and offer competitive salaries.

Real-Life Applications of Division and Fractions

Division and fractions have numerous real-life applications, from cooking and measuring ingredients to calculating the cost of goods or services. Some examples of real-life applications include:

Cooking: Division and fractions are essential for measuring ingredients and scaling recipes up or down.
Finance: Division and fractions are used to calculate interest rates, investment returns, and credit scores.
Science: Division and fractions are used to calculate quantities, such as the concentration of a solution or the velocity of an object.
Engineering: Division and fractions are used to design and build structures, such as bridges and buildings.

Steps to Master Division and Fractions

Mastering division and fractions requires practice, patience, and persistence. Here are some steps to help individuals master these concepts:

Start with the basics: Begin by understanding the concept of division and fractions, including the symbols and notation.
Practice regularly: Practice division and fractions regularly, using worksheets, online resources, or math games.
Use real-life examples: Use real-life examples to illustrate the concept of division and fractions, making it more relatable and interesting.
Break down complex problems: Break down complex problems into simpler steps, using division and fractions to solve each step.
Seek help when needed: Seek help from teachers, tutors, or online resources when needed, to clarify any doubts or misunderstandings.

Common Mistakes to Avoid

When working with division and fractions, there are common mistakes to avoid, such as:

Confusing the numerator and denominator: Make sure to understand the difference between the numerator and denominator, and use them correctly.
Not simplifying fractions: Simplify fractions to their simplest form, to avoid confusion and errors.
Not using the correct operation: Use the correct operation, whether it's division, multiplication, or addition, to solve the problem.
Not checking the units: Check the units of measurement, to ensure that they are consistent and accurate.

Conclusion and Next Steps

In conclusion, understanding division and fractions is essential for mathematical literacy and critical thinking. By mastering these concepts, individuals can develop a deeper understanding of mathematical relationships and apply them to real-life situations. To take the next step, individuals can practice regularly, use real-life examples, and seek help when needed. With persistence and dedication, anyone can master division and fractions, and unlock a world of mathematical possibilities.

Division and Fractions Image Gallery

What is division?

Division is a basic mathematical operation that involves sharing or grouping a certain quantity into equal parts.

What are fractions?

Fractions are a way of representing a part of a whole, and they are denoted by the symbol /.

How do I master division and fractions?

Mastering division and fractions requires practice, patience, and persistence. Start with the basics, practice regularly, and use real-life examples to illustrate the concepts.

What are some common mistakes to avoid when working with division and fractions?

Common mistakes to avoid include confusing the numerator and denominator, not simplifying fractions, not using the correct operation, and not checking the units.

Why are division and fractions important?

Division and fractions are essential for mathematical literacy and critical thinking. They have numerous real-life applications, from cooking and finance to science and engineering.

We hope this article has provided you with a comprehensive understanding of division and fractions, and how 6 goes into 18. Whether you're a student, teacher, or simply someone interested in mathematics, we encourage you to share your thoughts and experiences with us. Please comment below, share this article with your friends and family, or take a moment to practice your division and fractions skills. With persistence and dedication, anyone can master these essential mathematical concepts and unlock a world of possibilities.