Prime Factorization Of 105

The concept of prime factorization is a fundamental idea in mathematics, particularly in number theory. It involves breaking down a composite number into a product of prime numbers. In this case, we will explore the prime factorization of 105.

To begin with, let's understand what prime factorization is. Prime factorization is a way of expressing a number as a product of its prime factors. A prime number is a positive integer that is divisible only by itself and 1. For example, the prime factorization of 12 is 2^2 * 3, because 2 and 3 are prime numbers that multiply together to give 12.

Now, let's find the prime factorization of 105. To do this, we need to find the prime numbers that divide 105 without leaving a remainder. We can start by dividing 105 by the smallest prime number, which is 2. However, 105 is not divisible by 2, so we move on to the next prime number, which is 3. Again, 105 is not divisible by 3, so we move on to the next prime number, which is 5. This time, 105 is divisible by 5, giving us 105 ÷ 5 = 21.

Next, we need to find the prime factorization of 21. We can start by dividing 21 by the smallest prime number, which is 2. However, 21 is not divisible by 2, so we move on to the next prime number, which is 3. This time, 21 is divisible by 3, giving us 21 ÷ 3 = 7. Since 7 is a prime number, we have found the prime factorization of 21, which is 3 * 7.

Now, we can combine the prime factorization of 21 with the factor of 5 that we found earlier. Therefore, the prime factorization of 105 is 3 * 5 * 7.

Understanding Prime Factorization

In this section, we will delve deeper into the concept of prime factorization and its significance in mathematics. Prime factorization is a unique way of expressing a number, and it has numerous applications in various fields, including cryptography, coding theory, and number theory.

One of the key benefits of prime factorization is that it allows us to break down complex numbers into their simplest building blocks. This can be useful in a variety of situations, such as finding the greatest common divisor (GCD) of two numbers or determining the least common multiple (LCM) of two numbers.

For example, let's say we want to find the GCD of 105 and 30. To do this, we can start by finding the prime factorization of both numbers. The prime factorization of 105 is 3 * 5 * 7, and the prime factorization of 30 is 2 * 3 * 5. By comparing the two prime factorizations, we can see that the common factors are 3 and 5. Therefore, the GCD of 105 and 30 is 3 * 5 = 15.

Benefits of Prime Factorization

The benefits of prime factorization are numerous and varied. Some of the key advantages include:

Simplifying complex numbers: Prime factorization allows us to break down complex numbers into their simplest building blocks, making it easier to work with them.
Finding GCD and LCM: Prime factorization is useful for finding the GCD and LCM of two numbers, which has numerous applications in mathematics and computer science.
Cryptography: Prime factorization is used in cryptography to secure online transactions and communication.
Coding theory: Prime factorization is used in coding theory to develop error-correcting codes and detect errors in digital data.

Steps to Find Prime Factorization

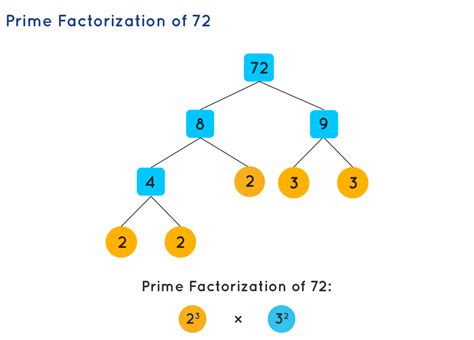
In this section, we will outline the steps to find the prime factorization of a number. The process is relatively straightforward and involves dividing the number by prime numbers until we reach 1.

Here are the steps to find the prime factorization of a number:

Start by dividing the number by the smallest prime number, which is 2.
If the number is divisible by 2, divide it by 2 and write down the factor.
Continue dividing the number by 2 until it is no longer divisible by 2.
Move on to the next prime number, which is 3, and repeat the process.
Continue dividing the number by prime numbers until we reach 1.
The prime factorization of the number is the product of all the prime factors.

For example, let's find the prime factorization of 100. We start by dividing 100 by 2, giving us 50. We continue dividing 50 by 2, giving us 25. Since 25 is not divisible by 2, we move on to the next prime number, which is 3. However, 25 is not divisible by 3, so we move on to the next prime number, which is 5. This time, 25 is divisible by 5, giving us 5. Since 5 is a prime number, we have found the prime factorization of 100, which is 2^2 * 5^2.

Common Mistakes to Avoid

When finding the prime factorization of a number, there are several common mistakes to avoid. Some of the key mistakes include:

Forgetting to divide by all prime numbers: Make sure to divide the number by all prime numbers until we reach 1.
Not writing down all the factors: Make sure to write down all the prime factors, including repeated factors.
Not checking for divisibility: Make sure to check if the number is divisible by each prime number before moving on to the next one.

Real-World Applications of Prime Factorization

In this section, we will explore the real-world applications of prime factorization. Prime factorization has numerous applications in various fields, including cryptography, coding theory, and number theory.

One of the key applications of prime factorization is in cryptography. Cryptography is the practice of secure online transactions and communication. Prime factorization is used in cryptography to develop secure encryption algorithms, such as RSA and elliptic curve cryptography.

Another application of prime factorization is in coding theory. Coding theory is the study of error-correcting codes and detection of errors in digital data. Prime factorization is used in coding theory to develop error-correcting codes, such as Reed-Solomon codes and BCH codes.

Prime factorization also has applications in number theory, particularly in the study of properties of numbers, such as primality and divisibility.

Future Developments

The field of prime factorization is constantly evolving, with new developments and advancements being made regularly. Some of the future developments in prime factorization include:

Improved algorithms: Researchers are working on developing improved algorithms for prime factorization, such as the general number field sieve and the elliptic curve method.
Quantum computing: The development of quantum computing has the potential to revolutionize the field of prime factorization, enabling faster and more efficient factorization of large numbers.
Applications in other fields: Prime factorization has the potential to be applied in other fields, such as physics and engineering, particularly in the study of complex systems and networks.

Gallery of Prime Factorization

Prime Factorization Image Gallery

FAQs

What is prime factorization?

Prime factorization is a way of expressing a number as a product of its prime factors.

Why is prime factorization important?

Prime factorization is important because it has numerous applications in various fields, including cryptography, coding theory, and number theory.

How do I find the prime factorization of a number?

To find the prime factorization of a number, start by dividing the number by the smallest prime number, which is 2, and continue dividing by prime numbers until we reach 1.

What are some common mistakes to avoid when finding prime factorization?

Some common mistakes to avoid when finding prime factorization include forgetting to divide by all prime numbers, not writing down all the factors, and not checking for divisibility.

What are some real-world applications of prime factorization?

Some real-world applications of prime factorization include cryptography, coding theory, and number theory, particularly in the study of properties of numbers, such as primality and divisibility.

In conclusion, prime factorization is a fundamental concept in mathematics that has numerous applications in various fields. By understanding the concept of prime factorization and its significance, we can appreciate the importance of this mathematical concept in our daily lives. Whether you are a student, a researcher, or simply someone interested in mathematics, prime factorization is a fascinating topic that is worth exploring further. So, take the time to learn more about prime factorization and its applications, and discover the beauty and complexity of this mathematical concept. We encourage you to share your thoughts and questions about prime factorization in the comments section below, and to share this article with others who may be interested in this topic.