Intro
Discover 5 ways to divide radicals with ease, using simplified radical expressions, rationalizing denominators, and conjugate pairs to master algebraic manipulation and solve complex equations efficiently.
Dividing radicals is a fundamental concept in algebra, and it's essential to understand the rules and procedures to simplify radical expressions. In this article, we'll explore the five ways to divide radicals, including the use of conjugates, rationalizing the denominator, and simplifying radical expressions.
Radicals are mathematical expressions that contain a square root or other roots, such as cube roots or fourth roots. When dividing radicals, we need to follow specific rules to ensure that the resulting expression is simplified and accurate. The five ways to divide radicals are:
- Dividing radicals with the same index
- Dividing radicals with different indices
- Using conjugates to divide radicals
- Rationalizing the denominator
- Simplifying radical expressions
These methods will help you to divide radicals with confidence and accuracy.
Dividing Radicals with the Same Index

When dividing radicals with the same index, we can simply divide the numbers inside the radical signs. For example, to divide √16 by √4, we can divide the numbers inside the radical signs: 16 ÷ 4 = 4. Therefore, √16 ÷ √4 = √4 = 2.
Dividing Radicals with Different Indices

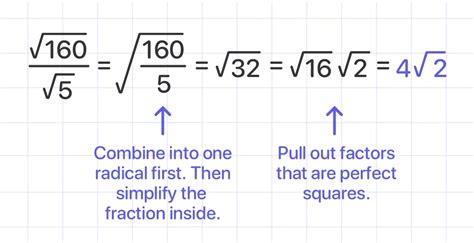
When dividing radicals with different indices, we need to rationalize the denominator by multiplying both the numerator and denominator by a radical that will eliminate the radical in the denominator. For example, to divide √16 by ∛4, we can multiply both the numerator and denominator by ∛4²: (√16 × ∛4²) ÷ (∛4 × ∛4²). This simplifies to (√16 × ∛16) ÷ (∛4³), which further simplifies to (√16 × ∛16) ÷ 4.
Using Conjugates to Divide Radicals

Conjugates are used to rationalize the denominator when dividing radicals. A conjugate is a radical expression that has the same terms as the original expression but with the opposite sign. For example, the conjugate of 2 + √3 is 2 - √3. To divide radicals using conjugates, we multiply both the numerator and denominator by the conjugate of the denominator. This will eliminate the radical in the denominator.
Rationalizing the Denominator

Rationalizing the denominator is an essential step when dividing radicals. To rationalize the denominator, we multiply both the numerator and denominator by a radical that will eliminate the radical in the denominator. This process ensures that the resulting expression is simplified and accurate.
Simplifying Radical Expressions

Simplifying radical expressions is crucial when dividing radicals. To simplify radical expressions, we look for perfect squares or perfect cubes that can be factored out of the radical sign. For example, √16 can be simplified to 4 because 16 is a perfect square. Similarly, ∛27 can be simplified to 3 because 27 is a perfect cube.
Benefits of Simplifying Radical Expressions
Simplifying radical expressions has several benefits, including:
- Easier calculations: Simplified radical expressions are easier to work with and calculate.
- Improved accuracy: Simplifying radical expressions reduces the chance of errors and ensures accuracy.
- Clearer understanding: Simplified radical expressions provide a clearer understanding of the underlying mathematical concepts.
Common Mistakes to Avoid
When dividing radicals, there are several common mistakes to avoid, including:
- Not rationalizing the denominator
- Not simplifying radical expressions
- Using the wrong conjugate
- Not following the order of operations
By avoiding these common mistakes, you can ensure that your calculations are accurate and your radical expressions are simplified.
Dividing Radicals Image Gallery


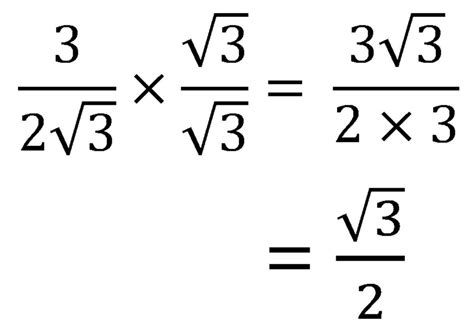





What is the first step in dividing radicals?
+The first step in dividing radicals is to determine if the radicals have the same index or different indices.
How do you rationalize the denominator when dividing radicals?
+To rationalize the denominator, multiply both the numerator and denominator by a radical that will eliminate the radical in the denominator.
What is the benefit of simplifying radical expressions?
+Simplifying radical expressions makes calculations easier, improves accuracy, and provides a clearer understanding of the underlying mathematical concepts.
How do you avoid common mistakes when dividing radicals?
+To avoid common mistakes, always rationalize the denominator, simplify radical expressions, use the correct conjugate, and follow the order of operations.
Can you divide radicals with variables?
+Yes, you can divide radicals with variables by following the same rules and procedures as dividing radicals with numbers.
In conclusion, dividing radicals requires a thorough understanding of the rules and procedures to simplify radical expressions. By following the five ways to divide radicals and avoiding common mistakes, you can ensure that your calculations are accurate and your radical expressions are simplified. We hope this article has provided you with a comprehensive understanding of dividing radicals and has helped you to become more confident in your mathematical abilities. If you have any further questions or would like to share your thoughts on dividing radicals, please don't hesitate to comment below.
