Intro
Discover the unique properties of a cone, where a single edge meets at the apex, exploring its geometric implications and mathematical concepts, including topology and geometry principles.
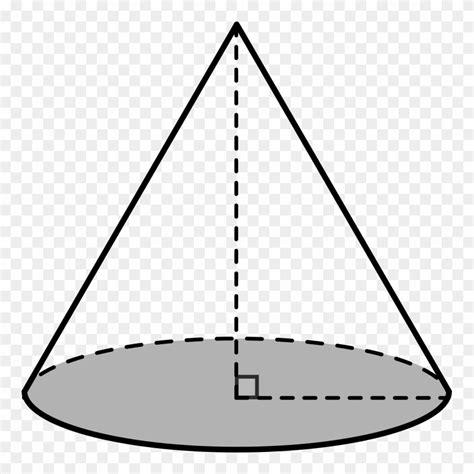
The concept of a cone having only one edge may seem counterintuitive at first, but it's a fundamental idea in geometry and mathematics. To understand this concept, let's dive into the world of shapes and dimensions. A cone is a three-dimensional shape that tapers from a circular base to a point, known as the apex. When we think of edges, we typically imagine a line where two surfaces meet. However, in the case of a cone, there is only one edge, which is the circular base.
This idea may be challenging to visualize, but it's essential to recognize that the cone's surface is continuous and unbroken, with no sharp corners or intersections. The edge of the cone is not a traditional edge, like the one found in a polygon, but rather a boundary that separates the cone's surface from the surrounding space. As we explore the properties of cones and their edges, we'll discover more about the fascinating world of geometry and its applications.
Introduction to Cones and Their Properties

Cones are an essential part of geometry, and their properties have numerous applications in various fields, including engineering, architecture, and design. A cone's shape is defined by its circular base and the apex, which is the point where the cone tapers to a single point. The surface of the cone is a continuous, curved shape that connects the base to the apex. One of the critical properties of a cone is its edge, which is the boundary between the cone's surface and the surrounding space.
Understanding the Concept of an Edge
In geometry, an edge is a line where two surfaces meet. However, in the case of a cone, there is only one edge, which is the circular base. This may seem counterintuitive, as we typically think of edges as lines where two surfaces intersect. But, in the case of a cone, the surface is continuous and unbroken, with no sharp corners or intersections. The edge of the cone is not a traditional edge, like the one found in a polygon, but rather a boundary that separates the cone's surface from the surrounding space.
Exploring the Properties of Cones

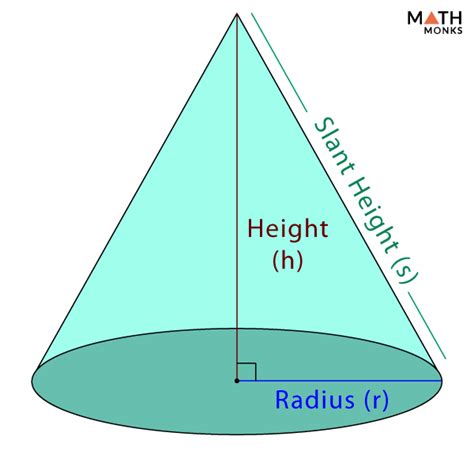
As we delve deeper into the properties of cones, we'll discover more about their dimensions, surface area, and volume. Cones are three-dimensional shapes, which means they have length, width, and height. The dimensions of a cone are defined by its radius, height, and slant height. The radius is the distance from the center of the base to the edge of the base, while the height is the distance from the apex to the base. The slant height is the distance from the apex to the edge of the base, and it's an essential dimension in calculating the surface area and volume of the cone.
Calculating the Surface Area and Volume of a Cone
The surface area of a cone is the total area of its surface, including the base and the curved surface. The formula for calculating the surface area of a cone is A = πr^2 + πrl, where A is the surface area, π is a mathematical constant, r is the radius, and l is the slant height. The volume of a cone is the amount of space inside the cone, and it's calculated using the formula V = (1/3)πr^2h, where V is the volume, π is a mathematical constant, r is the radius, and h is the height.
Applications of Cones in Real-World Scenarios

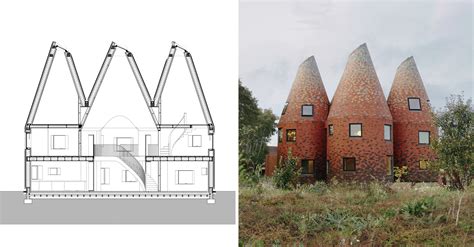
Cones have numerous applications in various fields, including engineering, architecture, and design. In engineering, cones are used in the design of roofs, bridges, and other structures. The shape of a cone provides excellent strength and stability, making it an ideal choice for structures that need to withstand heavy loads. In architecture, cones are used in the design of buildings, monuments, and other structures. The shape of a cone adds a unique and aesthetically pleasing element to a building's design.
Real-World Examples of Cones
One of the most famous examples of a cone is the Eiffel Tower in Paris, France. The tower's shape is a cone, with a circular base and a tapering shape that rises to a point. The Eiffel Tower is an excellent example of the strength and stability of a cone shape. Another example of a cone is a roof of a building. Many buildings have cone-shaped roofs, which provide excellent protection from the elements and add a unique element to the building's design.
Gallery of Cone-Related Images
Cone Image Gallery






Frequently Asked Questions
What is a cone in geometry?
+A cone is a three-dimensional shape that tapers from a circular base to a point, known as the apex.
What is the edge of a cone?
+The edge of a cone is the circular base, which is the boundary between the cone's surface and the surrounding space.
What are some real-world applications of cones?
+Cones have numerous applications in various fields, including engineering, architecture, and design. They are used in the design of roofs, bridges, and other structures, and add a unique element to a building's design.
How is the surface area of a cone calculated?
+The surface area of a cone is calculated using the formula A = πr^2 + πrl, where A is the surface area, π is a mathematical constant, r is the radius, and l is the slant height.
What is the volume of a cone?
+The volume of a cone is the amount of space inside the cone, and it's calculated using the formula V = (1/3)πr^2h, where V is the volume, π is a mathematical constant, r is the radius, and h is the height.
In conclusion, the concept of a cone having only one edge is a fundamental idea in geometry and mathematics. As we've explored the properties of cones, their applications, and real-world examples, we've gained a deeper understanding of the importance of cones in various fields. Whether you're an engineer, architect, or simply someone interested in geometry, the study of cones is a fascinating and rewarding topic. We encourage you to continue exploring the world of cones and their many applications, and to share your thoughts and questions with us in the comments below.
