Pentagon Exterior Angles Explained

The pentagon is a fascinating geometric shape that has been studied for centuries. One of the key aspects of a pentagon is its exterior angles, which play a crucial role in understanding the properties and behavior of this five-sided shape. In this article, we will delve into the world of pentagon exterior angles, exploring their definition, calculation, and significance in various mathematical and real-world contexts.

A pentagon is a polygon with five sides, and like all polygons, it has exterior angles that are formed by extending each side of the shape. These exterior angles are essential in geometry, as they help us understand the relationships between different parts of a shape and how they interact with each other. The exterior angles of a pentagon are particularly interesting, as they have unique properties that set them apart from other polygons.

The study of pentagon exterior angles is not only important in mathematics but also has practical applications in various fields, such as architecture, engineering, and design. By understanding the properties and behavior of pentagon exterior angles, we can create more efficient and effective designs, from buildings and bridges to electronic circuits and computer graphics. In this article, we will explore the concept of pentagon exterior angles in detail, providing examples, formulas, and illustrations to help readers grasp this fundamental concept in geometry.

What are Pentagon Exterior Angles?

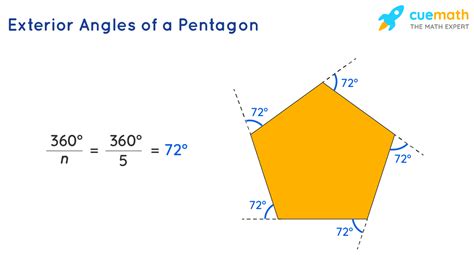
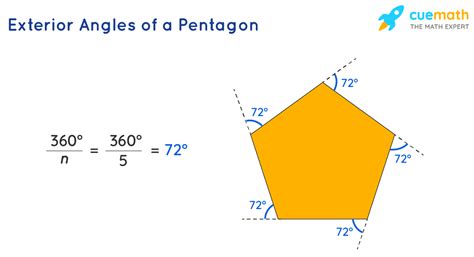
Pentagon exterior angles are the angles formed by extending each side of a pentagon. These angles are external to the shape and are measured in degrees. The sum of the exterior angles of a pentagon is always 360 degrees, which is a fundamental property of all polygons. This means that if we extend each side of a pentagon and measure the angles formed, the total sum of these angles will always be 360 degrees.

To calculate the exterior angles of a pentagon, we can use the formula: Exterior Angle = 360° / Number of Sides. In the case of a pentagon, which has five sides, the exterior angle would be 360° / 5 = 72°. This means that each exterior angle of a regular pentagon measures 72 degrees.

Properties of Pentagon Exterior Angles

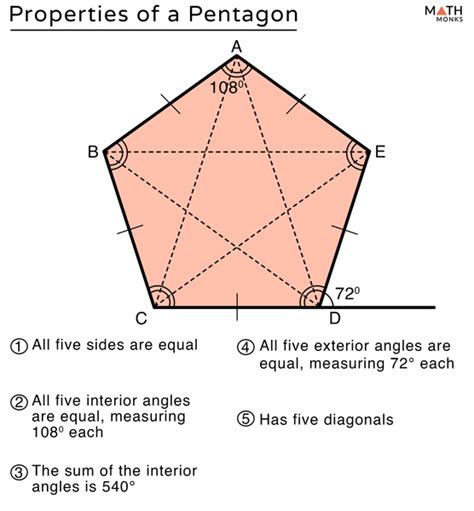
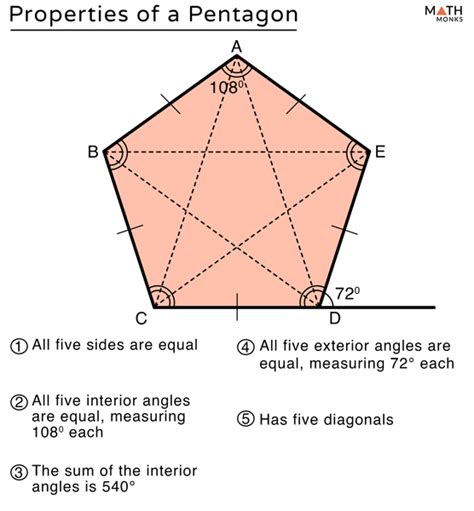
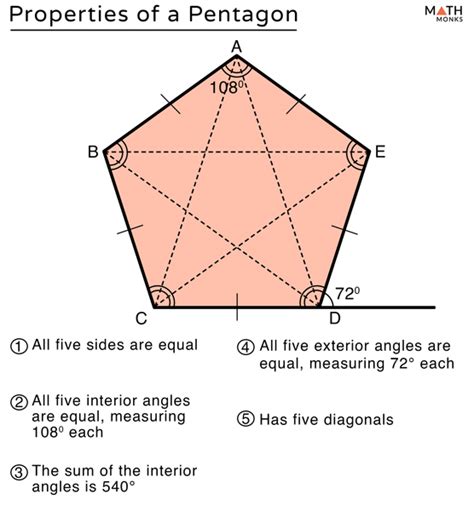
Pentagon exterior angles have several interesting properties that make them unique. One of the most important properties is that the sum of the exterior angles of a pentagon is always 360 degrees. This property is true for all polygons, regardless of the number of sides.

Another property of pentagon exterior angles is that they are equal in measure if the pentagon is regular. A regular pentagon is a pentagon with all sides and angles equal. In a regular pentagon, each exterior angle measures 72 degrees, as calculated earlier.

Pentagon exterior angles also have a relationship with the interior angles of the shape. The sum of an exterior angle and its corresponding interior angle is always 180 degrees. This property is useful in calculating the interior angles of a pentagon, given the exterior angles.

Types of Pentagon Exterior Angles

There are two types of pentagon exterior angles: regular and irregular. Regular pentagon exterior angles are equal in measure and are found in regular pentagons. Irregular pentagon exterior angles are unequal in measure and are found in irregular pentagons.

Regular pentagon exterior angles are important in geometry and have many practical applications. They are used in the design of buildings, bridges, and other structures, where symmetry and balance are essential.

Irregular pentagon exterior angles, on the other hand, are used in more complex designs, where unique shapes and angles are required. They are also used in computer graphics and animation, where irregular shapes and angles are used to create realistic models and simulations.

Calculating Pentagon Exterior Angles

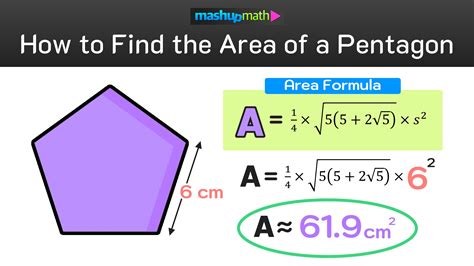
Calculating pentagon exterior angles is a straightforward process that involves using the formula: Exterior Angle = 360° / Number of Sides. In the case of a pentagon, which has five sides, the exterior angle would be 360° / 5 = 72°.

To calculate the exterior angles of an irregular pentagon, we need to use the formula: Exterior Angle = 180° - Interior Angle. This formula requires us to know the interior angles of the pentagon, which can be calculated using the formula: Interior Angle = (n-2) × 180° / n, where n is the number of sides.

Once we have the interior angles, we can calculate the exterior angles using the formula: Exterior Angle = 180° - Interior Angle. This will give us the measure of each exterior angle, which can be used in various mathematical and real-world applications.

Real-World Applications of Pentagon Exterior Angles

Pentagon exterior angles have many real-world applications, from architecture and engineering to computer graphics and animation. They are used in the design of buildings, bridges, and other structures, where symmetry and balance are essential.

In architecture, pentagon exterior angles are used to create unique and aesthetically pleasing designs. They are used in the design of buildings, such as the Pentagon building in Washington D.C., which is a famous example of a pentagonal structure.

In engineering, pentagon exterior angles are used in the design of bridges, tunnels, and other infrastructure projects. They are used to create strong and stable structures that can withstand various types of stress and strain.

In computer graphics and animation, pentagon exterior angles are used to create realistic models and simulations. They are used to create 3D models of buildings, bridges, and other structures, which are used in video games, movies, and other forms of entertainment.

Conclusion and Future Directions

In conclusion, pentagon exterior angles are a fundamental concept in geometry that has many practical applications. They are used in architecture, engineering, computer graphics, and animation, and have many unique properties that make them essential in various mathematical and real-world contexts.

As we continue to explore and understand the properties and behavior of pentagon exterior angles, we can expect to see new and innovative applications in various fields. From the design of more efficient and effective structures to the creation of more realistic models and simulations, the study of pentagon exterior angles will continue to play a vital role in shaping our world.

Gallery of Pentagon Exterior Angles

Pentagon Exterior Angles Image Gallery

$Pentagon Math Diagram$

What is the sum of the exterior angles of a pentagon?

The sum of the exterior angles of a pentagon is always 360 degrees.

How do you calculate the exterior angles of a pentagon?

To calculate the exterior angles of a pentagon, you can use the formula: Exterior Angle = 360° / Number of Sides. In the case of a pentagon, which has five sides, the exterior angle would be 360° / 5 = 72°.

What are some real-world applications of pentagon exterior angles?

What is the difference between regular and irregular pentagon exterior angles?

Regular pentagon exterior angles are equal in measure and are found in regular pentagons. Irregular pentagon exterior angles are unequal in measure and are found in irregular pentagons.

How do pentagon exterior angles relate to interior angles?

The sum of an exterior angle and its corresponding interior angle is always 180 degrees. This property is useful in calculating the interior angles of a pentagon, given the exterior angles.

We hope this article has provided you with a comprehensive understanding of pentagon exterior angles and their significance in various mathematical and real-world contexts. Whether you are a student, teacher, or professional, we encourage you to share your thoughts and experiences with pentagon exterior angles in the comments section below. Additionally, we invite you to share this article with others who may be interested in learning more about this fascinating topic. By working together, we can continue to explore and understand the many wonders of geometry and its applications in our world.