5 Ways To Divide 67 By 12

Dividing numbers is a fundamental mathematical operation that we use in our daily lives. When it comes to dividing 67 by 12, there are several ways to approach this problem. In this article, we will explore five different methods to divide 67 by 12.

Dividing numbers can be challenging, especially when dealing with fractions or decimals. However, with the right approach, anyone can master this mathematical operation. Whether you are a student, a professional, or simply someone who wants to improve your mathematical skills, this article is for you. We will provide you with a comprehensive guide on how to divide 67 by 12 using different methods.

The importance of learning how to divide numbers cannot be overstated. Division is a crucial mathematical operation that is used in various aspects of our lives, from cooking and shopping to science and engineering. By mastering the art of division, you can improve your problem-solving skills, enhance your critical thinking, and become more confident in your ability to tackle mathematical challenges.

Introduction to Division

Before we dive into the different methods of dividing 67 by 12, let's take a brief look at the concept of division. Division is a mathematical operation that involves sharing a certain quantity into equal parts. It is the inverse operation of multiplication, meaning that it undoes the operation of multiplication. For example, if we multiply 12 by 5, we get 60. If we divide 60 by 12, we get 5.

Method 1: Long Division

The first method we will explore is long division. Long division is a step-by-step process that involves dividing a dividend by a divisor to get a quotient and a remainder. To divide 67 by 12 using long division, we start by dividing the dividend (67) by the divisor (12). We can do this by dividing the first digit of the dividend (6) by the divisor (12). Since 12 does not go into 6, we move to the next digit (7) and divide 67 by 12.

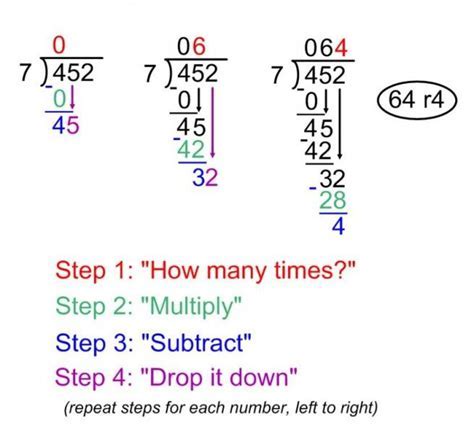
Step-by-Step Long Division

Here are the steps to divide 67 by 12 using long division: * Divide the first digit of the dividend (6) by the divisor (12). Since 12 does not go into 6, we move to the next digit (7). * Divide 67 by 12. We get 5 with a remainder of 7. * Write the quotient (5) and the remainder (7) as a fraction (5 7/12).

Method 2: Short Division

The second method we will explore is short division. Short division is a simplified version of long division that involves dividing a dividend by a divisor to get a quotient and a remainder. To divide 67 by 12 using short division, we can use a calculator or perform the calculation mentally. We divide 67 by 12 and get 5.58.

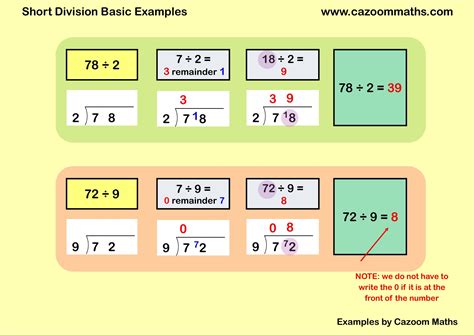
Step-by-Step Short Division

Here are the steps to divide 67 by 12 using short division: * Divide 67 by 12 using a calculator or perform the calculation mentally. * Get the quotient (5.58) and round it to the nearest whole number or decimal place.

Method 3: Fractional Division

The third method we will explore is fractional division. Fractional division involves dividing a fraction by another fraction. To divide 67 by 12 using fractional division, we can convert the dividend (67) to a fraction (67/1) and the divisor (12) to a fraction (12/1). We then invert the divisor (12/1) to get (1/12) and multiply the dividend (67/1) by the inverted divisor (1/12).

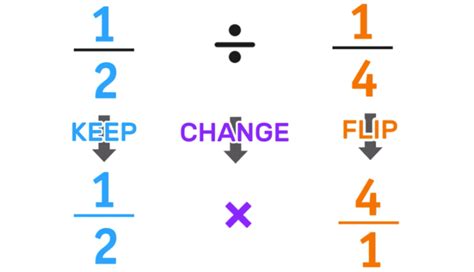
Step-by-Step Fractional Division

Here are the steps to divide 67 by 12 using fractional division: * Convert the dividend (67) to a fraction (67/1) and the divisor (12) to a fraction (12/1). * Invert the divisor (12/1) to get (1/12). * Multiply the dividend (67/1) by the inverted divisor (1/12) to get (67/12).

Method 4: Decimal Division

The fourth method we will explore is decimal division. Decimal division involves dividing a decimal number by another decimal number. To divide 67 by 12 using decimal division, we can convert the dividend (67) to a decimal number (67.0) and the divisor (12) to a decimal number (12.0). We then divide the decimal dividend (67.0) by the decimal divisor (12.0) to get the quotient (5.58).

Step-by-Step Decimal Division

Here are the steps to divide 67 by 12 using decimal division: * Convert the dividend (67) to a decimal number (67.0) and the divisor (12) to a decimal number (12.0). * Divide the decimal dividend (67.0) by the decimal divisor (12.0) to get the quotient (5.58).

Method 5: Mental Math

The fifth method we will explore is mental math. Mental math involves performing mathematical calculations in your head without using a calculator or pen and paper. To divide 67 by 12 using mental math, we can use estimation techniques such as rounding the dividend (67) to the nearest multiple of the divisor (12). We can round 67 to 60, which is a multiple of 12 (12 x 5 = 60). We then divide 60 by 12 to get 5 and adjust the quotient to account for the remainder (7).

Step-by-Step Mental Math

Here are the steps to divide 67 by 12 using mental math: * Round the dividend (67) to the nearest multiple of the divisor (12). * Divide the rounded dividend (60) by the divisor (12) to get the quotient (5). * Adjust the quotient to account for the remainder (7).

Division Methods Image Gallery

What is the difference between long division and short division?

+

Long division is a step-by-step process that involves dividing a dividend by a divisor to get a quotient and a remainder. Short division is a simplified version of long division that involves dividing a dividend by a divisor to get a quotient and a remainder without going through the step-by-step process.

How do I perform mental math division?

+

To perform mental math division, you can use estimation techniques such as rounding the dividend to the nearest multiple of the divisor. You can then divide the rounded dividend by the divisor to get the quotient and adjust the quotient to account for the remainder.

What are the benefits of learning division?

+

The benefits of learning division include improving problem-solving skills, enhancing critical thinking, and becoming more confident in your ability to tackle mathematical challenges. Division is a fundamental mathematical operation that is used in various aspects of our lives, from cooking and shopping to science and engineering.

How do I choose the right division method for a problem?

+

The choice of division method depends on the problem and your personal preference. If you need to perform a complex division, long division may be the best method. If you need to perform a simple division, short division or mental math may be the best method.

Can I use a calculator to perform division?

+

Yes, you can use a calculator to perform division. However, it's also important to learn how to perform division manually using different methods such as long division, short division, and mental math. This will help you develop your problem-solving skills and become more confident in your ability to tackle mathematical challenges.

In conclusion, dividing 67 by 12 can be done using different methods such as long division, short division, fractional division, decimal division, and mental math. Each method has its own advantages and disadvantages, and the choice of method depends on the problem and your personal preference. By mastering the different division methods, you can improve your problem-solving skills, enhance your critical thinking, and become more confident in your ability to tackle mathematical challenges. We hope this article has been helpful in explaining the different methods of dividing 67 by 12. If you have any questions or comments, please don't hesitate to reach out to us. Share this article with your friends and family to help them improve their mathematical skills.