Intro
Calculate 3 to the 6th power with our detailed guide, covering exponentiation, mathematical operations, and power calculations for precise results and understanding of numerical values and equations.
The concept of exponentiation is a fundamental aspect of mathematics, and understanding how to calculate powers of numbers is essential for various applications in science, engineering, and finance. In this article, we will delve into the calculation of 3 to the 6th power, exploring the underlying principles and providing a step-by-step guide on how to perform this calculation.
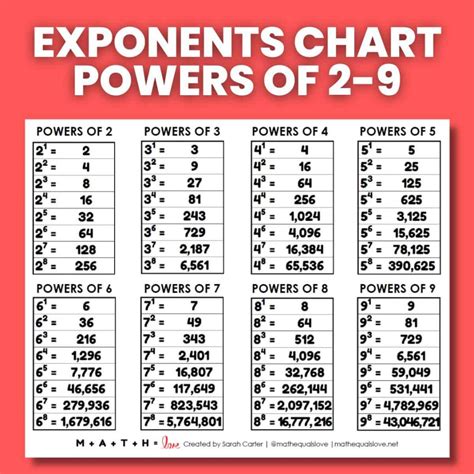
When we talk about exponentiation, we are essentially dealing with the operation of raising a number, known as the base, to a certain power, represented by an exponent. In the case of 3 to the 6th power, the base is 3, and the exponent is 6. The result of this operation is obtained by multiplying the base by itself as many times as indicated by the exponent. Therefore, 3 to the 6th power can be calculated as 3 * 3 * 3 * 3 * 3 * 3.
Understanding Exponentiation
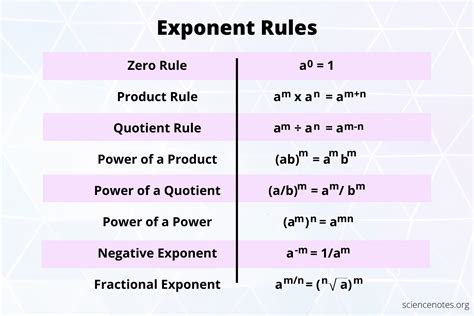
Exponentiation is a shorthand way of writing repeated multiplication. For instance, 3^6 is equivalent to 3 * 3 * 3 * 3 * 3 * 3. This notation is useful for representing large numbers and simplifying complex calculations. The properties of exponentiation, such as the product of powers property and the power of a power property, allow us to manipulate and simplify expressions involving exponents.
Calculating 3 to the 6th Power
To calculate 3 to the 6th power, we can use the following steps:
- Start with the base number, which is 3.
- Multiply the base by itself 6 times: 3 * 3 * 3 * 3 * 3 * 3.
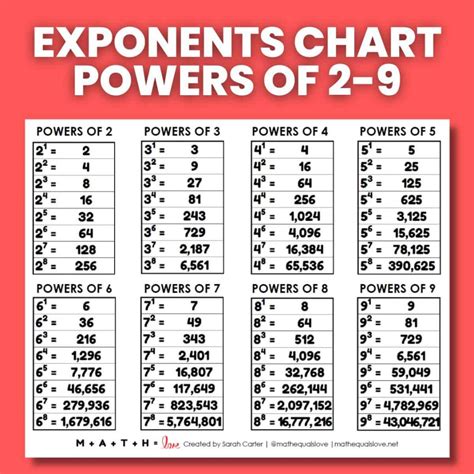
- Perform the multiplication operation: 3 * 3 = 9, 9 * 3 = 27, 27 * 3 = 81, 81 * 3 = 243, 243 * 3 = 729.
Step-by-Step Calculation
The calculation of 3 to the 6th power involves repeated multiplication of the base number. Here's a breakdown of the steps: * 3 * 3 = 9 * 9 * 3 = 27 * 27 * 3 = 81 * 81 * 3 = 243 * 243 * 3 = 729Properties of Exponentiation
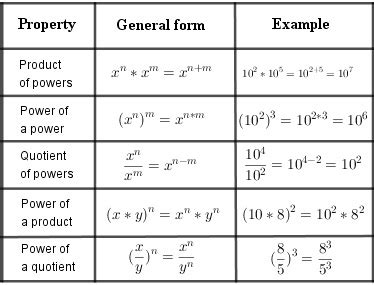
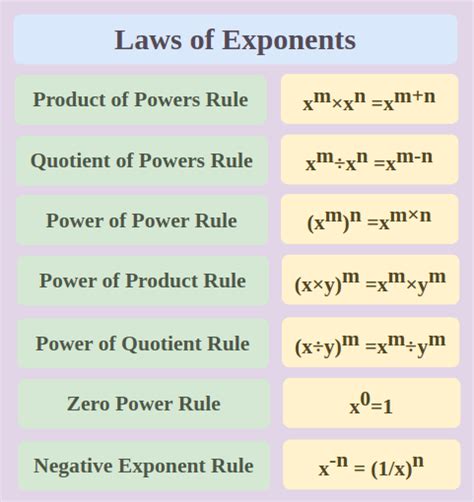
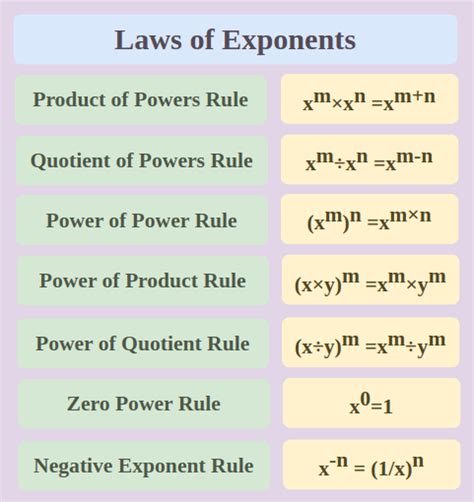
The properties of exponentiation are essential for simplifying expressions and performing calculations involving exponents. Some key properties include:
- The product of powers property: a^m * a^n = a^(m+n)
- The power of a power property: (a^m)^n = a^(m*n)
- The zero exponent property: a^0 = 1
Applications of Exponentiation
Exponentiation has numerous applications in various fields, including:
- Science: exponential growth and decay models
- Engineering: calculations involving exponential functions
- Finance: compound interest and investment calculations
Conclusion and Final Thoughts

In conclusion, calculating 3 to the 6th power involves understanding the concept of exponentiation and applying the properties of exponents. By following the step-by-step guide and using the properties of exponentiation, we can simplify expressions and perform calculations involving exponents. Exponentiation is a fundamental concept in mathematics, and its applications are diverse and widespread.
Gallery of Exponentiation
Exponentiation Image Gallery





What is exponentiation?
+Exponentiation is a mathematical operation that involves raising a number, called the base, to a certain power, represented by an exponent.
How do you calculate 3 to the 6th power?
+To calculate 3 to the 6th power, you multiply the base (3) by itself 6 times: 3 * 3 * 3 * 3 * 3 * 3.
What are the properties of exponentiation?
+The properties of exponentiation include the product of powers property, the power of a power property, and the zero exponent property.
We hope this article has provided you with a comprehensive understanding of the concept of exponentiation and how to calculate 3 to the 6th power. If you have any further questions or would like to share your thoughts on the topic, please don't hesitate to comment below. Additionally, if you found this article informative and helpful, please consider sharing it with others who may benefit from this knowledge.
